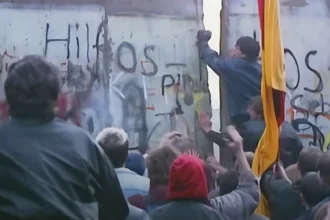Les décisions politiques à travers une lentille mathématique
Mathematics in Politics and Governance vise à présenter les outils mathématiques que les politiciens utilisent le plus souvent pour prendre des décisions en matière de santé, d'éducation, de culture, d'économie, de finances, de transport ou de défense nationale ; c'est-à-dire des décisions politiques et de gouvernance qui affectent directement les citoyens.
La sélection des sujets abordés repose sur les expériences raisonnées de quatre politiciens chevronnés titulaires de doctorats ou de maîtrises en mathématiques : l'ancien Premier ministre d'Israël Ehud Barak, l'ancien ministre espagnol des Travaux publics et des Affaires étrangères, et actuel Haut représentant de l'Union européenne pour les Affaires étrangères et la Politique de sécurité, Josep Borrell, l'ancienne ministre allemande Johanna Wanka, et l'ancien ministre portugais Nuno Crato, tous deux responsables des ministères de l'Éducation et de la Science.
Perspectives mathématiques des leaders politiques
Barak et Borrell ont expliqué comment ils ont utilisé leur formation mathématique pour prendre des décisions politiques dans My Country, My Life: Fighting for Israel, Searching for Peace (MacMillan, 2018) et The Republic of Taxonia [en espagnol] (Pirámide, 1992), respectivement.
À son tour, Crato a contribué à Mathematics in Politics and Governance avec un extrait expliquant comment il a utilisé des outils statistiques pour réformer avec succès le système éducatif portugais.
Grâce aux techniques d'optimisation, à l'analyse statistique et aux applications de big data, les modèles mathématiques offrent des solutions aux gouvernements, aux institutions et aux décideurs politiques.
Wanka, quant à elle, a collaboré au livre en fournissant un aperçu des applications connues et potentielles des mathématiques à la prise de décision politique. Ceci est présenté sous la forme d'un dialogue avec son mari, le mathématicien Gert Wanka. En raison de ces contributions, ainsi que d'autres commentaires, documents et critiques constructives fournies par de nombreux collègues et amis (comme mentionné dans les Remerciements), nous pouvons affirmer que le livre est le résultat d'un effort collectif pour apporter la rationalité à la politique et à la gouvernance.
Le livre ne considère pas seulement les outils mathématiques utilisés pour prendre des décisions politiques et de gouvernance, mais aussi ceux utilisés pour capter des votes ou pour optimiser leur impact effectif par le biais de la conception ad hoc des circonscriptions électorales afin d'augmenter le nombre de représentants (le gerrymandering), et, seulement de manière incidente, les mathématiques appliquées à l'activité parlementaire que les citoyens perçoivent comme éloignée de leurs intérêts. Le dernier chapitre inverse la perspective des précédents pour analyser l'impact significatif des décisions politiques sur le développement des mathématiques dans une sélection de pays et de communautés discriminées.
En ce qui concerne les connaissances mathématiques nécessaires pour profiter pleinement du livre, les chapitres 1 et 6 sont accessibles à tous les lecteurs, tandis que les chapitres 2 à 5 supposent un niveau de mathématiques de lycée, sauf pour les sections marquées par des astérisques, qui exigent une compréhension de niveau universitaire. Néanmoins, nous pensons que les lecteurs peuvent bénéficier de l'ensemble du livre, même si certains détails mathématiques se révèlent difficiles, tout comme on peut apprécier une pièce musicale sans saisir chaque parole.
Outils mathématiques pour la prise de décision politique
Les mathématiques jouent un rôle de plus en plus crucial dans la prise de décisions politiques, fournissant des outils pour relever des défis complexes allant de la planification économique à la stratégie électorale.
La faisabilité des décisions politiques dépend souvent de la capacité à répondre à une série d'exigences pratiques.
Grâce aux techniques d'optimisation, à l'analyse statistique et aux applications de big data, les modèles mathématiques offrent des solutions aux gouvernements, aux institutions et aux décideurs politiques.
Dans notre livre, nous explorons un éventail d'outils mathématiques et leurs applications pratiques dans des contextes politiques, en mettant en évidence des cas clés où ces méthodes ont influencé des décisions et des résultats au niveau national et international.
- Dialogue entre Johanna et Gert Wanka : Une discussion centrée sur les applications des mathématiques dans des contextes politiques.
- Utilisation des outils d'optimisation par Borrell : Lors de son mandat à la tête du Secrétariat d'État aux Finances et du Ministère des Travaux publics en Espagne, Borrell a largement appliqué des techniques d'optimisation pour améliorer la prise de décision.
- Conseil de Crato à un nouveau ministre de l'Éducation : Dans sa Lettre à un jeune ministre : Quelques choses que j'aurais aimé savoir lorsque j'ai pris mes fonctions (2019), Crato donne des conseils sur l'utilisation stratégique des outils statistiques dans l'élaboration des politiques.
- Mensonges statistiques des politiciens : Les exemples incluent des données trompeuses utilisées par des figures telles que Nixon, Trump, Biden, López Obrador, Obama et Bolsonaro, ainsi que des manipulations par les chaînes de télévision et les institutions de régulation.
- Échec de la dissuasion nucléaire pendant la Guerre froide : Analyse des failles de la stratégie de dissuasion nucléaire, ainsi que de la tentative d'Ehud Barak d'obtenir une paix durable avec Yasser Arafat lors du sommet de Camp David en 2000, promu par Bill Clinton.
Faisabilité (ou comment répondre aux exigences)
La faisabilité des décisions politiques dépend souvent de la capacité à répondre à une série d'exigences pratiques, qui peuvent être abordées par des modèles mathématiques tels que les systèmes linéaires représentant des polyèdres.
Voici quelques exemples notables de la manière dont les mathématiques ont été appliquées pour relever divers défis logistiques et de planification :
- Polyèdres dans les soins de santé : Comment les modèles mathématiques ont aidé à relever des défis tels que la lutte contre les épidémies ou l'affectation des hôpitaux aux patients.
- Mobilité citoyenne : La conception de lignes de métro qui préservent les monuments, illustrant l'équilibre entre les besoins en infrastructures et le patrimoine culturel.
- La planification de Leontief après le krach de Wall Street de 1929 : Utilisation de modèles mathématiques pour planifier la croissance économique des États-Unis.
- Les décisions logistiques du Pentagone jusqu'en 1945 : Résolution des défis logistiques par des systèmes linéaires, une application clé des mathématiques de la faisabilité.
Optimisation scalaire (ou comment prendre la meilleure décision)
L'optimisation scalaire est essentielle pour prendre les meilleures décisions face à des ressources limitées. Ce chapitre examine des exemples historiques clés de la manière dont ces techniques d'optimisation ont façonné les stratégies politiques et économiques :
- La méthode de George Dantzig (1946) : Concevoir une méthode pour planifier la logistique du Pentagone en minimisant des fonctions linéaires sur des polyèdres.
- Mécanisation de la planification économique : Le groupe de Dantzig a obtenu des financements du Pentagone pour le développement de l'informatique en 1949, ouvrant la voie à une optimisation accrue dans la planification économique.
- Réfutation de la tarification marginaliste de l'électricité en Europe : Les modèles mathématiques ont remis en question les systèmes de tarification établis, démontrant le pouvoir de l'optimisation.
Optimisation vectorielle (ou comment prendre des décisions insurmontables)
L'optimisation vectorielle concerne des décisions impliquant plusieurs objectifs, souvent en concurrence. Nous explorons comment les modèles mathématiques ont été appliqués pour résoudre des problèmes complexes avec des objectifs contradictoires :
- Protection du patrimoine archéologique sous-marin : Résoudre un problème d'optimisation avec deux objectifs : maximiser la probabilité de localiser des épaves tout en minimisant le temps nécessaire pour le faire.
- Combinaison d'indices en indices composites : Utilisation de la méthode de Dantzig pour créer des indices composites, que Crato a appliqués pour assigner des enseignants aux écoles portugaises.
- Localisation des bateaux de recherche et de sauvetage en Turquie : Application de modèles d'optimisation pour positionner stratégiquement les ressources de sauvetage.
Big data (ou comment décider en utilisant des informations massives)
En la era del big data, la toma de decisiones políticas depende cada vez más del procesamiento a gran escala de información. Este capítulo analiza el uso del muestreo, la investigación operativa y el aprendizaje automático para abordar diversos desafíos políticos y sociales:
- Échantillonnage et recherche opérationnelle dans les campagnes électorales : Application de ces techniques pour optimiser les stratégies de campagne.
- Apprentissage automatique en santé, économie et science politique : Des exemples incluent le diagnostic automatique, la détection de faillite et même la linguistique légale (par exemple, découvrir l'identité derrière le pseudonyme QAnon).
- Détection de l'idéologie politique avec des réseaux neuronaux : Une nouvelle frontière en science politique où des réseaux neuronaux sont utilisés pour analyser les tendances idéologiques.
- Apprendre à gagner des élections : Appliquer l'apprentissage automatique aux campagnes électorales, y compris le cas controversé du travail de Cambridge Analytica avec les données de Facebook.
- Lutter contre le gerrymandering : Utiliser des modèles mathématiques et des analyses de big data pour contester les délimitations électorales injustes devant les tribunaux.
L'impact des décisions politiques sur les mathématiques
Le développement des mathématiques a été profondément façonné par les circonstances historiques et politiques au fil des siècles. De l'essor des mathématiques en Union soviétique à l'impact de la Révolution française sur l'intégration des Juifs dans la vie académique, le cours de l'histoire a laissé une empreinte indélébile sur l'évolution de cette discipline. Voici des exemples clés illustrant comment différents contextes sociopolitiques ont influencé l'avancement et la pratique des mathématiques à diverses époques et en divers lieux.
- Les années dorées des mathématiques russes : Malgré le risque de sévères punitions pour dissidence depuis le virage de Staline (1928-1931), les mathématiques soviétiques ont atteint leur âge d'or dans les années 1960. Quelles conditions politiques et culturelles ont permis cet essor des réalisations mathématiques ?
- Le talent juif après l'abolition des ghettos : L'abolition des ghettos après la Révolution française a libéré une vague de talent juif en mathématiques. Cependant, les lois discriminatoires en Allemagne entre 1932 et 1939 ont réduit drastiquement le nombre d'étudiants juifs en mathématiques de 82 %.
- L'essor des mathématiciens hongrois : La compétition de mathématiques Eötvös, établie en 1894, a déclenché une tradition d'excellence mathématique en Hongrie. Ce modèle de compétition a été imité dans les pays voisins et est devenu un phénomène mondial impliquant des millions de participants.
- L'enfer est pavé de bonnes intentions : En réaction au succès du Spoutnik soviétique dans les années 1960, les autorités américaines ont introduit un nouveau programme mathématique structuraliste. Cependant, la mise en œuvre des « mathématiques modernes » a été si rapide que les éducateurs ont eu du mal à suivre le rythme du matériel.
- L'exil des mathématiciens hispaniques : Les monarques espagnols ont historiquement pris des décisions visant à défendre l'Église catholique contre les infidèles et les sceptiques, entraînant des exils massifs. Cela inclut l'expulsion des Juifs en 1492, des Musulmans en 1609 et des libéraux politiques en 1823. L'exode des meilleurs mathématiciens espagnols vers l'Argentine pendant le régime de Franco a été aggravé par la dictature argentine (1976-1983), où jusqu'à 50 % des scientifiques ont été contraints à l'exil.
- Les hauts et les bas des mathématiques chinoises : La rébellion des Boxers (1899-1900) et les réparations de guerre qui ont suivi ont conduit les États-Unis à créer les Bourses d'indemnisation des Boxers, amenant plus de 900 étudiants chinois aux États-Unis entre 1911 et 1929. Cependant, les progrès accomplis dans les mathématiques chinoises ont été annulés par la Révolution culturelle (1966-1976).
- Interférences politiques dans les mathématiques turques : Mustafa Kemal Atatürk a réformé les mathématiques turques en rédigeant personnellement le manuel Géométrie. Cependant, sous la présidence d'Erdoğan, l'enthousiasme pour faire progresser les mathématiques a diminué, avec seulement trois mathématiciens parmi les près de 200 membres de l'Académie turque des sciences.
- Discrimination raciale : L'Université Howard (1867) et l'Université catholique d'Amérique (1889, brièvement CUA) ont été parmi les premières à accepter des étudiants afro-américains, bien que la CUA ait inversé sa politique en 1914 en raison des pressions ségrégationnistes, rétablissant les politiques d'admission interraciales deux décennies plus tard. Malgré ces défis, plusieurs institutions historiquement noires ont produit des mathématiciens hautement qualifiés, comme les trois femmes afro-américaines qui ont contribué au programme spatial de la NASA dans les années 1960, inspirant le film Les Figures de l'ombre. Le Potsdam College, sous la direction de Clarence Stephens, est devenu la troisième institution comptant le plus grand nombre de majors en mathématiques aux États-Unis à la fin du XXe siècle.
- Discrimination de genre : Au XIXe siècle et au-delà, les femmes n'étaient pas autorisées à entrer dans les universités européennes. La situation s'est naturellement améliorée avec l'accès massif des femmes au marché du travail pendant la Seconde Guerre mondiale pour remplacer les travailleurs mobilisés. Un exemple notable est celui des 80 femmes de l'Université de Pennsylvanie, également appelées « calculatrices » par la Marine, qui pendant la guerre ont résolu, à la main et en utilisant des calculatrices de bureau mécaniques, les équations différentielles partielles complexes issues de la balistique. À la fin du projet ENIAC, le groupe de femmes s'est dispersé, mais elles ont collaboré à la construction d'autres ordinateurs tels que le BINAC et l'UNIVAC (le premier ordinateur commercial), ainsi qu'à la conception des premiers langages de programmation, COBOL et FORTRAN.
Conclusion
Bien que le talent mathématique soit intrinsèquement et uniformément réparti dans le monde entier, il n'en va pas de même pour les opportunités. Les barrières historiques, sociales et politiques ont longtemps restreint l'accès à l'éducation et à l'avancement, en particulier pour les groupes marginalisés. Les gouvernements — tant dans les pays occidentaux qu'ailleurs — font face au défi constant de garantir un accès équitable à l'éducation et aux ressources.
Pour remédier à ce déséquilibre, un engagement soutenu est nécessaire pour démanteler les barrières systémiques et promouvoir des systèmes éducatifs inclusifs permettant à chaque individu, quel que soit son origine, de développer et d'appliquer son potentiel mathématique. Ce n'est qu'à travers de tels efforts que nous pourrons espérer parvenir à une véritable répartition équitable des opportunités.
